| Contents [0/19] |
| Video [1/19] |
| XCountingLoops [2/19] |
| 2D Square [3/19] |
| 2D Triangle [4/19] |
| 2D Flat Pack [5/19] |
| 2D N * lg(N) [6/19] |
| 2D N * lg(N) - Flat Pack [7/19] |
| 2D lg(N) * lg(N) [8/19] |
| 3D Cube [9/19] |
| 3D Pyramid [10/19] |
| 4D Cube [11/19] |
| 4D Pyramid [12/19] |
| 5D Cube [13/19] |
| 5D Pyramid [14/19] |
| XCountingRecursion [15/19] |
| Recursive Factorial [16/19] |
| Recursive Fibonacci (Terrible Version) [17/19] |
| String Concatenation (Recursive) [18/19] |
| String Concatenation (Loop) [19/19] |
(Click here for one slide per page)
| Video [1/19] |
In three parts
| XCountingLoops [2/19] |
file:XCountingLoops.java [source] [doc-public] [doc-private]
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| 2D Square [3/19] |
01 |
for (long i = 1; i <= N; i = i+1) { for (long j = 1; j <= N; j = j+1) { result = result+1; } } |
Output
01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 02 02 02 02 02 02 02 02 02 02 02 02 02 02 02 02 03 03 03 03 03 03 03 03 03 03 03 03 03 03 03 03 04 04 04 04 04 04 04 04 04 04 04 04 04 04 04 04 05 05 05 05 05 05 05 05 05 05 05 05 05 05 05 05 06 06 06 06 06 06 06 06 06 06 06 06 06 06 06 06 07 07 07 07 07 07 07 07 07 07 07 07 07 07 07 07 08 08 08 08 08 08 08 08 08 08 08 08 08 08 08 08 09 09 09 09 09 09 09 09 09 09 09 09 09 09 09 09 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 13 13 13 13 13 13 13 13 13 13 13 13 13 13 13 13 14 14 14 14 14 14 14 14 14 14 14 14 14 14 14 14 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 Elapsed count f( 512): 262,144: 4.000 [ 0.003 : 0.750] Elapsed count f( 1,024): 1,048,576: 4.000 [ 0.001 : 0.333] Elapsed count f( 2,048): 4,194,304: 4.000 [ 0.006 : 6.000] Elapsed count f( 4,096): 16,777,216: 4.000 [ 0.032 : 5.333] Elapsed count f( 8,192): 67,108,864: 4.000 [ 0.056 : 1.750] Elapsed count f( 16,384): 268,435,456: 4.000 [ 0.152 : 2.714] Elapsed count f( 32,768): 1,073,741,824: 4.000 [ 0.546 : 3.592] Elapsed count f( 65,536): 4,294,967,296: 4.000 [ 2.228 : 4.081] Elapsed count f( 131,072): 17,179,869,184: 4.000 [ 9.405 : 4.221] Elapsed count f( 262,144): 68,719,476,736: 4.000 [ 35.069 : 3.729] Elapsed count f( 524,288) aborted execution after a minute or so Elapsed count f( 1,048,576) aborted execution after a minute or so Elapsed count f( 2,097,152) aborted execution after a minute or so Elapsed count f( 4,194,304) aborted execution after a minute or so Elapsed count f( 8,388,608) aborted execution after a minute or so Elapsed count f( 16,777,216) aborted execution after a minute or so Elapsed count f( 33,554,432) aborted execution after a minute or so Elapsed count f( 67,108,864) aborted execution after a minute or so Elapsed count f( 134,217,728) aborted execution after a minute or so Elapsed count f( 268,435,456) aborted execution after a minute or so Elapsed count f( 536,870,912) aborted execution after a minute or so Elapsed count f(1,073,741,824) aborted execution after a minute or so Elapsed count f(2,147,483,648) aborted execution after a minute or so
This is quadratic: ~ N^2
| 2D Triangle [4/19] |
01 |
for (long i = 1; i <= N; i = i+1) { for (long j = 1; j <= i; j = j+1) { result = result+1; } } |
Output
01 02 02 03 03 03 04 04 04 04 05 05 05 05 05 06 06 06 06 06 06 07 07 07 07 07 07 07 08 08 08 08 08 08 08 08 09 09 09 09 09 09 09 09 09 10 10 10 10 10 10 10 10 10 10 11 11 11 11 11 11 11 11 11 11 11 12 12 12 12 12 12 12 12 12 12 12 12 13 13 13 13 13 13 13 13 13 13 13 13 13 14 14 14 14 14 14 14 14 14 14 14 14 14 14 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 Elapsed count f( 512): 131,328: 3.992 [ 0.002 : 2.000] Elapsed count f( 1,024): 524,800: 3.996 [ 0.003 : 1.500] Elapsed count f( 2,048): 2,098,176: 3.998 [ 0.002 : 0.667] Elapsed count f( 4,096): 8,390,656: 3.999 [ 0.005 : 2.500] Elapsed count f( 8,192): 33,558,528: 4.000 [ 0.016 : 3.200] Elapsed count f( 16,384): 134,225,920: 4.000 [ 0.065 : 4.063] Elapsed count f( 32,768): 536,887,296: 4.000 [ 0.246 : 3.785] Elapsed count f( 65,536): 2,147,516,416: 4.000 [ 1.001 : 4.069] Elapsed count f( 131,072): 8,590,000,128: 4.000 [ 4.006 : 4.002] Elapsed count f( 262,144): 34,359,869,440: 4.000 [ 15.628 : 3.901] Elapsed count f( 524,288): 137,439,215,616: 4.000 [ 62.422 : 3.994] Elapsed count f( 1,048,576) aborted execution after a minute or so Elapsed count f( 2,097,152) aborted execution after a minute or so Elapsed count f( 4,194,304) aborted execution after a minute or so Elapsed count f( 8,388,608) aborted execution after a minute or so Elapsed count f( 16,777,216) aborted execution after a minute or so Elapsed count f( 33,554,432) aborted execution after a minute or so Elapsed count f( 67,108,864) aborted execution after a minute or so Elapsed count f( 134,217,728) aborted execution after a minute or so Elapsed count f( 268,435,456) aborted execution after a minute or so Elapsed count f( 536,870,912) aborted execution after a minute or so Elapsed count f(1,073,741,824) aborted execution after a minute or so Elapsed count f(2,147,483,648) aborted execution after a minute or so
This is quadratic: ~ 1/2 * N^2
More accurately: (1/2 * N^2) - N/2
| 2D Flat Pack [5/19] |
01 |
for (long i = 1; i <= N; i = i*2) { for (long j = 1; j <= i; j = j+1) { result = result+1; } } |
Output
01 02 02 04 04 04 04 08 08 08 08 08 08 08 08 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 Elapsed count f( 512): 1,023: 2.002 [ 0.000 : NaN] Elapsed count f( 1,024): 2,047: 2.001 [ 0.000 : NaN] Elapsed count f( 2,048): 4,095: 2.000 [ 0.001 : Infinity] Elapsed count f( 4,096): 8,191: 2.000 [ 0.000 : 0.000] Elapsed count f( 8,192): 16,383: 2.000 [ 0.001 : Infinity] Elapsed count f( 16,384): 32,767: 2.000 [ 0.003 : 3.000] Elapsed count f( 32,768): 65,535: 2.000 [ 0.001 : 0.333] Elapsed count f( 65,536): 131,071: 2.000 [ 0.003 : 3.000] Elapsed count f( 131,072): 262,143: 2.000 [ 0.000 : 0.000] Elapsed count f( 262,144): 524,287: 2.000 [ 0.001 : Infinity] Elapsed count f( 524,288): 1,048,575: 2.000 [ 0.001 : 1.000] Elapsed count f( 1,048,576): 2,097,151: 2.000 [ 0.002 : 2.000] Elapsed count f( 2,097,152): 4,194,303: 2.000 [ 0.003 : 1.500] Elapsed count f( 4,194,304): 8,388,607: 2.000 [ 0.010 : 3.333] Elapsed count f( 8,388,608): 16,777,215: 2.000 [ 0.019 : 1.900] Elapsed count f( 16,777,216): 33,554,431: 2.000 [ 0.033 : 1.737] Elapsed count f( 33,554,432): 67,108,863: 2.000 [ 0.041 : 1.242] Elapsed count f( 67,108,864): 134,217,727: 2.000 [ 0.092 : 2.244] Elapsed count f( 134,217,728): 268,435,455: 2.000 [ 0.169 : 1.837] Elapsed count f( 268,435,456): 536,870,911: 2.000 [ 0.292 : 1.728] Elapsed count f( 536,870,912): 1,073,741,823: 2.000 [ 0.553 : 1.894] Elapsed count f(1,073,741,824): 2,147,483,647: 2.000 [ 1.149 : 2.078] Elapsed count f(2,147,483,648): 4,294,967,295: 2.000 [ 2.284 : 1.988]
This is linear: ~ 2N
More accurately: 2N - 1
| 2D N * lg(N) [6/19] |
01 |
for (long i = 1; i <= N; i = i*2) { for (long j = 1; j <= N; j = j+1) { result = result+1; } } |
Output
01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 02 02 02 02 02 02 02 02 02 02 02 02 02 02 02 02 04 04 04 04 04 04 04 04 04 04 04 04 04 04 04 04 08 08 08 08 08 08 08 08 08 08 08 08 08 08 08 08 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 Elapsed count f( 512): 5,120: 2.222 [ 0.000 : NaN] Elapsed count f( 1,024): 11,264: 2.200 [ 0.001 : Infinity] Elapsed count f( 2,048): 24,576: 2.182 [ 0.001 : 1.000] Elapsed count f( 4,096): 53,248: 2.167 [ 0.001 : 1.000] Elapsed count f( 8,192): 114,688: 2.154 [ 0.000 : 0.000] Elapsed count f( 16,384): 245,760: 2.143 [ 0.002 : Infinity] Elapsed count f( 32,768): 524,288: 2.133 [ 0.001 : 0.500] Elapsed count f( 65,536): 1,114,112: 2.125 [ 0.001 : 1.000] Elapsed count f( 131,072): 2,359,296: 2.118 [ 0.001 : 1.000] Elapsed count f( 262,144): 4,980,736: 2.111 [ 0.003 : 3.000] Elapsed count f( 524,288): 10,485,760: 2.105 [ 0.006 : 2.000] Elapsed count f( 1,048,576): 22,020,096: 2.100 [ 0.014 : 2.333] Elapsed count f( 2,097,152): 46,137,344: 2.095 [ 0.030 : 2.143] Elapsed count f( 4,194,304): 96,468,992: 2.091 [ 0.054 : 1.800] Elapsed count f( 8,388,608): 201,326,592: 2.087 [ 0.108 : 2.000] Elapsed count f( 16,777,216): 419,430,400: 2.083 [ 0.222 : 2.056] Elapsed count f( 33,554,432): 872,415,232: 2.080 [ 0.505 : 2.275] Elapsed count f( 67,108,864): 1,811,939,328: 2.077 [ 0.972 : 1.925] Elapsed count f( 134,217,728): 3,758,096,384: 2.074 [ 2.057 : 2.116] Elapsed count f( 268,435,456): 7,784,628,224: 2.071 [ 4.106 : 1.996] Elapsed count f( 536,870,912): 16,106,127,360: 2.069 [ 8.241 : 2.007] Elapsed count f(1,073,741,824): 33,285,996,544: 2.067 [ 17.254 : 2.094] Elapsed count f(2,147,483,648): 68,719,476,736: 2.065 [ 35.660 : 2.067]
This is linearithmic: ~ N * lg(N)
| 2D N * lg(N) - Flat Pack [7/19] |
01 |
for (long i = 1; i <= N; i = i*2) { for (long j = i + 1; j <= N; j = j+1) { result = result+1; } } |
Output
01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 02 02 02 02 02 02 02 02 02 02 02 02 02 02 04 04 04 04 04 04 04 04 04 04 04 04 08 08 08 08 08 08 08 08 Elapsed count f( 512): 4,097: 2.285 [ 0.001 : Infinity] Elapsed count f( 1,024): 9,217: 2.250 [ 0.001 : 1.000] Elapsed count f( 2,048): 20,481: 2.222 [ 0.001 : 1.000] Elapsed count f( 4,096): 45,057: 2.200 [ 0.001 : 1.000] Elapsed count f( 8,192): 98,305: 2.182 [ 0.000 : 0.000] Elapsed count f( 16,384): 212,993: 2.167 [ 0.001 : Infinity] Elapsed count f( 32,768): 458,753: 2.154 [ 0.001 : 1.000] Elapsed count f( 65,536): 983,041: 2.143 [ 0.000 : 0.000] Elapsed count f( 131,072): 2,097,153: 2.133 [ 0.002 : Infinity] Elapsed count f( 262,144): 4,456,449: 2.125 [ 0.003 : 1.500] Elapsed count f( 524,288): 9,437,185: 2.118 [ 0.006 : 2.000] Elapsed count f( 1,048,576): 19,922,945: 2.111 [ 0.013 : 2.167] Elapsed count f( 2,097,152): 41,943,041: 2.105 [ 0.026 : 2.000] Elapsed count f( 4,194,304): 88,080,385: 2.100 [ 0.057 : 2.192] Elapsed count f( 8,388,608): 184,549,377: 2.095 [ 0.145 : 2.544] Elapsed count f( 16,777,216): 385,875,969: 2.091 [ 0.260 : 1.793] Elapsed count f( 33,554,432): 805,306,369: 2.087 [ 0.517 : 1.988] Elapsed count f( 67,108,864): 1,677,721,601: 2.083 [ 1.020 : 1.973] Elapsed count f( 134,217,728): 3,489,660,929: 2.080 [ 2.126 : 2.084] Elapsed count f( 268,435,456): 7,247,757,313: 2.077 [ 4.608 : 2.167] Elapsed count f( 536,870,912): 15,032,385,537: 2.074 [ 9.334 : 2.026] Elapsed count f(1,073,741,824): 31,138,512,897: 2.071 [ 19.133 : 2.050] Elapsed count f(2,147,483,648): 64,424,509,441: 2.069 [ 40.003 : 2.091]
This is linearithmic: ~ N * lg(N)
More accurately: (N * lg(N)) - (2N - 1)
| 2D lg(N) * lg(N) [8/19] |
01 |
for (long i = 1; i <= N; i = i*2) { for (long j = 1; j <= N; j = j*2) { result = result+1; } } |
Output
01 01 01 01 01 02 02 02 02 02 04 04 04 04 04 08 08 08 08 08 16 16 16 16 16 Elapsed count f( 512): 100: 1.235 [ 0.000 : NaN] Elapsed count f( 1,024): 121: 1.210 [ 0.000 : NaN] Elapsed count f( 2,048): 144: 1.190 [ 0.000 : NaN] Elapsed count f( 4,096): 169: 1.174 [ 0.000 : NaN] Elapsed count f( 8,192): 196: 1.160 [ 0.000 : NaN] Elapsed count f( 16,384): 225: 1.148 [ 0.000 : NaN] Elapsed count f( 32,768): 256: 1.138 [ 0.000 : NaN] Elapsed count f( 65,536): 289: 1.129 [ 0.000 : NaN] Elapsed count f( 131,072): 324: 1.121 [ 0.000 : NaN] Elapsed count f( 262,144): 361: 1.114 [ 0.000 : NaN] Elapsed count f( 524,288): 400: 1.108 [ 0.000 : NaN] Elapsed count f( 1,048,576): 441: 1.103 [ 0.000 : NaN] Elapsed count f( 2,097,152): 484: 1.098 [ 0.000 : NaN] Elapsed count f( 4,194,304): 529: 1.093 [ 0.000 : NaN] Elapsed count f( 8,388,608): 576: 1.089 [ 0.000 : NaN] Elapsed count f( 16,777,216): 625: 1.085 [ 0.000 : NaN] Elapsed count f( 33,554,432): 676: 1.082 [ 0.000 : NaN] Elapsed count f( 67,108,864): 729: 1.078 [ 0.000 : NaN] Elapsed count f( 134,217,728): 784: 1.075 [ 0.000 : NaN] Elapsed count f( 268,435,456): 841: 1.073 [ 0.000 : NaN] Elapsed count f( 536,870,912): 900: 1.070 [ 0.001 : Infinity] Elapsed count f(1,073,741,824): 961: 1.068 [ 0.000 : 0.000] Elapsed count f(2,147,483,648): 1,024: 1.066 [ 0.000 : NaN]
This is log squared: ~ lg(N) * lg(N)
| 3D Cube [9/19] |
01 |
for (long i = 1; i <= N; i = i+1) { for (long j = 1; j <= N; j = j+1) { for (long k = 1; k <= N; k = k+1) { result = result+1; } } } |
Output
Elapsed count f( 8): 512: 8.000 [ 0.000 : NaN] Elapsed count f( 16): 4,096: 8.000 [ 0.000 : NaN] Elapsed count f( 32): 32,768: 8.000 [ 0.000 : NaN] Elapsed count f( 64): 262,144: 8.000 [ 0.001 : Infinity] Elapsed count f( 128): 2,097,152: 8.000 [ 0.004 : 4.000] Elapsed count f( 256): 16,777,216: 8.000 [ 0.008 : 2.000] Elapsed count f( 512): 134,217,728: 8.000 [ 0.063 : 7.875] Elapsed count f( 1,024): 1,073,741,824: 8.000 [ 0.532 : 8.444] Elapsed count f( 2,048): 8,589,934,592: 8.000 [ 3.979 : 7.479] Elapsed count f( 4,096): 68,719,476,736: 8.000 [ 31.300 : 7.866] Elapsed count f( 8,192): 549,755,813,888: 8.000 [ 253.206 : 8.090] Elapsed count f( 16,384) aborted execution after a minute or so Elapsed count f( 32,768) aborted execution after a minute or so Elapsed count f( 65,536) aborted execution after a minute or so Elapsed count f( 131,072) aborted execution after a minute or so Elapsed count f( 262,144) aborted execution after a minute or so Elapsed count f( 524,288) aborted execution after a minute or so Elapsed count f( 1,048,576) aborted execution after a minute or so Elapsed count f( 2,097,152) aborted execution after a minute or so Elapsed count f( 4,194,304) aborted execution after a minute or so Elapsed count f( 8,388,608) aborted execution after a minute or so Elapsed count f( 16,777,216) aborted execution after a minute or so Elapsed count f( 33,554,432) aborted execution after a minute or so Elapsed count f( 67,108,864) aborted execution after a minute or so Elapsed count f( 134,217,728) aborted execution after a minute or so Elapsed count f( 268,435,456) aborted execution after a minute or so Elapsed count f( 536,870,912) aborted execution after a minute or so Elapsed count f(1,073,741,824) aborted execution after a minute or so Elapsed count f(2,147,483,648) aborted execution after a minute or so
This is cubic: ~ N^3
| 3D Pyramid [10/19] |
01 |
for (long i = 1; i <= N; i = i+1) { for (long j = 1; j <= i; j = j+1) { for (long k = 1; k <= j; k = k+1) { result = result+1; } } } |
Output
Elapsed count f( 8): 120: 6.000 [ 0.000 : NaN] Elapsed count f( 16): 816: 6.800 [ 0.000 : NaN] Elapsed count f( 32): 5,984: 7.333 [ 0.000 : NaN] Elapsed count f( 64): 45,760: 7.647 [ 0.001 : Infinity] Elapsed count f( 128): 357,760: 7.818 [ 0.001 : 1.000] Elapsed count f( 256): 2,829,056: 7.908 [ 0.005 : 5.000] Elapsed count f( 512): 22,500,864: 7.953 [ 0.011 : 2.200] Elapsed count f( 1,024): 179,481,600: 7.977 [ 0.091 : 8.273] Elapsed count f( 2,048): 1,433,753,600: 7.988 [ 0.683 : 7.505] Elapsed count f( 4,096): 11,461,636,096: 7.994 [ 5.322 : 7.792] Elapsed count f( 8,192): 91,659,526,144: 7.997 [ 42.736 : 8.030] Elapsed count f( 16,384) aborted execution after a minute or so Elapsed count f( 32,768) aborted execution after a minute or so Elapsed count f( 65,536) aborted execution after a minute or so Elapsed count f( 131,072) aborted execution after a minute or so Elapsed count f( 262,144) aborted execution after a minute or so Elapsed count f( 524,288) aborted execution after a minute or so Elapsed count f( 1,048,576) aborted execution after a minute or so Elapsed count f( 2,097,152) aborted execution after a minute or so Elapsed count f( 4,194,304) aborted execution after a minute or so Elapsed count f( 8,388,608) aborted execution after a minute or so Elapsed count f( 16,777,216) aborted execution after a minute or so Elapsed count f( 33,554,432) aborted execution after a minute or so Elapsed count f( 67,108,864) aborted execution after a minute or so Elapsed count f( 134,217,728) aborted execution after a minute or so Elapsed count f( 268,435,456) aborted execution after a minute or so Elapsed count f( 536,870,912) aborted execution after a minute or so Elapsed count f(1,073,741,824) aborted execution after a minute or so Elapsed count f(2,147,483,648) aborted execution after a minute or so
This is cubic: ~ 1/6 * N^3
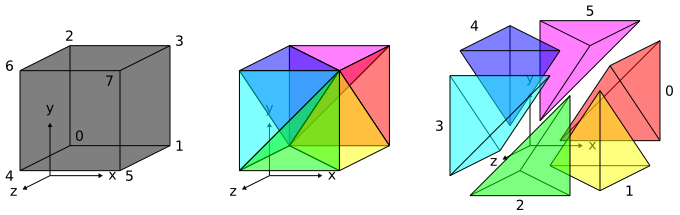
It's a tetrahedron (image from Dune Project):

| 4D Cube [11/19] |
01 |
for (long i = 1; i <= N; i = i+1) { for (long j = 1; j <= N; j = j+1) { for (long k = 1; k <= N; k = k+1) { for (long l = 1; l <= N; l = l+1) { result = result+1; } } } } |
Output
Elapsed count f( 8): 4,096: 16.000 [ 0.000 : NaN] Elapsed count f( 16): 65,536: 16.000 [ 0.000 : NaN] Elapsed count f( 32): 1,048,576: 16.000 [ 0.003 : Infinity] Elapsed count f( 64): 16,777,216: 16.000 [ 0.026 : 8.667] Elapsed count f( 128): 268,435,456: 16.000 [ 0.140 : 5.385] Elapsed count f( 256): 4,294,967,296: 16.000 [ 2.014 : 14.386] Elapsed count f( 512): 68,719,476,736: 16.000 [ 31.673 : 15.726] Elapsed count f( 1,024) aborted execution after a minute or so Elapsed count f( 2,048) aborted execution after a minute or so Elapsed count f( 4,096) aborted execution after a minute or so Elapsed count f( 8,192) aborted execution after a minute or so Elapsed count f( 16,384) aborted execution after a minute or so Elapsed count f( 32,768) aborted execution after a minute or so Elapsed count f( 65,536) aborted execution after a minute or so Elapsed count f( 131,072) aborted execution after a minute or so Elapsed count f( 262,144) aborted execution after a minute or so Elapsed count f( 524,288) aborted execution after a minute or so Elapsed count f( 1,048,576) aborted execution after a minute or so Elapsed count f( 2,097,152) aborted execution after a minute or so Elapsed count f( 4,194,304) aborted execution after a minute or so Elapsed count f( 8,388,608) aborted execution after a minute or so Elapsed count f( 16,777,216) aborted execution after a minute or so Elapsed count f( 33,554,432) aborted execution after a minute or so Elapsed count f( 67,108,864) aborted execution after a minute or so Elapsed count f( 134,217,728) aborted execution after a minute or so Elapsed count f( 268,435,456) aborted execution after a minute or so Elapsed count f( 536,870,912) aborted execution after a minute or so Elapsed count f(1,073,741,824) aborted execution after a minute or so Elapsed count f(2,147,483,648) aborted execution after a minute or so
This is quartic: ~ N^4
| 4D Pyramid [12/19] |
01 |
for (long i = 1; i <= N; i = i+1) { for (long j = 1; j <= i; j = j+1) { for (long k = 1; k <= j; k = k+1) { for (long l = 1; l <= k; l = l+1) { result = result+1; } } } } |
Output
Elapsed count f( 8): 330: 9.429 [ 0.000 : NaN] Elapsed count f( 16): 3,876: 11.745 [ 0.001 : Infinity] Elapsed count f( 32): 52,360: 13.509 [ 0.001 : 1.000] Elapsed count f( 64): 766,480: 14.639 [ 0.002 : 2.000] Elapsed count f( 128): 11,716,640: 15.286 [ 0.008 : 4.000] Elapsed count f( 256): 183,181,376: 15.634 [ 0.277 : 34.625] Elapsed count f( 512): 2,896,986,240: 15.815 [ 4.417 : 15.946] Elapsed count f( 1,024): 46,081,900,800: 15.907 [ 68.227 : 15.446] Elapsed count f( 2,048) aborted execution after a minute or so Elapsed count f( 4,096) aborted execution after a minute or so Elapsed count f( 8,192) aborted execution after a minute or so Elapsed count f( 16,384) aborted execution after a minute or so Elapsed count f( 32,768) aborted execution after a minute or so Elapsed count f( 65,536) aborted execution after a minute or so Elapsed count f( 131,072) aborted execution after a minute or so Elapsed count f( 262,144) aborted execution after a minute or so Elapsed count f( 524,288) aborted execution after a minute or so Elapsed count f( 1,048,576) aborted execution after a minute or so Elapsed count f( 2,097,152) aborted execution after a minute or so Elapsed count f( 4,194,304) aborted execution after a minute or so Elapsed count f( 8,388,608) aborted execution after a minute or so Elapsed count f( 16,777,216) aborted execution after a minute or so Elapsed count f( 33,554,432) aborted execution after a minute or so Elapsed count f( 67,108,864) aborted execution after a minute or so Elapsed count f( 134,217,728) aborted execution after a minute or so Elapsed count f( 268,435,456) aborted execution after a minute or so Elapsed count f( 536,870,912) aborted execution after a minute or so Elapsed count f(1,073,741,824) aborted execution after a minute or so Elapsed count f(2,147,483,648) aborted execution after a minute or so
This is quartic: ~ 1/24 * N^4
| 5D Cube [13/19] |
01 |
for (long i = 1; i <= N; i = i+1) { for (long j = 1; j <= N; j = j+1) { for (long k = 1; k <= N; k = k+1) { for (long l = 1; l <= N; l = l+1) { for (long m = 1; m <= N; m = m+1) { result = result+1; } } } } } |
Output
Elapsed count f( 8): 32,768: 32.000 [ 0.000 : NaN] Elapsed count f( 16): 1,048,576: 32.000 [ 0.000 : NaN] Elapsed count f( 32): 33,554,432: 32.000 [ 0.014 : Infinity] Elapsed count f( 64): 1,073,741,824: 32.000 [ 0.620 : 44.286] Elapsed count f( 128): 34,359,738,368: 32.000 [ 17.720 : 28.581] Elapsed count f( 256) aborted execution after a minute or so Elapsed count f( 512) aborted execution after a minute or so Elapsed count f( 1,024) aborted execution after a minute or so Elapsed count f( 2,048) aborted execution after a minute or so Elapsed count f( 4,096) aborted execution after a minute or so Elapsed count f( 8,192) aborted execution after a minute or so Elapsed count f( 16,384) aborted execution after a minute or so Elapsed count f( 32,768) aborted execution after a minute or so Elapsed count f( 65,536) aborted execution after a minute or so Elapsed count f( 131,072) aborted execution after a minute or so Elapsed count f( 262,144) aborted execution after a minute or so Elapsed count f( 524,288) aborted execution after a minute or so Elapsed count f( 1,048,576) aborted execution after a minute or so Elapsed count f( 2,097,152) aborted execution after a minute or so Elapsed count f( 4,194,304) aborted execution after a minute or so Elapsed count f( 8,388,608) aborted execution after a minute or so Elapsed count f( 16,777,216) aborted execution after a minute or so Elapsed count f( 33,554,432) aborted execution after a minute or so Elapsed count f( 67,108,864) aborted execution after a minute or so Elapsed count f( 134,217,728) aborted execution after a minute or so Elapsed count f( 268,435,456) aborted execution after a minute or so Elapsed count f( 536,870,912) aborted execution after a minute or so Elapsed count f(1,073,741,824) aborted execution after a minute or so Elapsed count f(2,147,483,648) aborted execution after a minute or so
This is quintic: ~ N^5
| 5D Pyramid [14/19] |
01 |
for (long i = 1; i <= N; i = i+1) { for (long j = 1; j <= i; j = j+1) { for (long k = 1; k <= j; k = k+1) { for (long l = 1; l <= k; l = l+1) { for (long m = 1; m <= l; m = m+1) { result = result+1; } } } } } |
Output
Elapsed count f( 8): 792: 14.143 [ 0.000 : NaN] Elapsed count f( 16): 15,504: 19.576 [ 0.001 : Infinity] Elapsed count f( 32): 376,992: 24.316 [ 0.003 : 3.000] Elapsed count f( 64): 10,424,128: 27.651 [ 0.018 : 6.000] Elapsed count f( 128): 309,319,296: 29.673 [ 0.491 : 27.278] Elapsed count f( 256): 9,525,431,552: 30.795 [ 5.574 : 11.352] Elapsed count f( 512) aborted execution after a minute or so Elapsed count f( 1,024) aborted execution after a minute or so Elapsed count f( 2,048) aborted execution after a minute or so Elapsed count f( 4,096) aborted execution after a minute or so Elapsed count f( 8,192) aborted execution after a minute or so Elapsed count f( 16,384) aborted execution after a minute or so Elapsed count f( 32,768) aborted execution after a minute or so Elapsed count f( 65,536) aborted execution after a minute or so Elapsed count f( 131,072) aborted execution after a minute or so Elapsed count f( 262,144) aborted execution after a minute or so Elapsed count f( 524,288) aborted execution after a minute or so Elapsed count f( 1,048,576) aborted execution after a minute or so Elapsed count f( 2,097,152) aborted execution after a minute or so Elapsed count f( 4,194,304) aborted execution after a minute or so Elapsed count f( 8,388,608) aborted execution after a minute or so Elapsed count f( 16,777,216) aborted execution after a minute or so Elapsed count f( 33,554,432) aborted execution after a minute or so Elapsed count f( 67,108,864) aborted execution after a minute or so Elapsed count f( 134,217,728) aborted execution after a minute or so Elapsed count f( 268,435,456) aborted execution after a minute or so Elapsed count f( 536,870,912) aborted execution after a minute or so Elapsed count f(1,073,741,824) aborted execution after a minute or so Elapsed count f(2,147,483,648) aborted execution after a minute or so
This is quintic: ~ 1/120 * N^5
| XCountingRecursion [15/19] |
file:XCountingRecursion.java [source] [doc-public] [doc-private]
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| Recursive Factorial [16/19] |
01 |
public static long f (long N) { if (N <= 1) { return 1; } else { long result = f(N-1) * N; numOps = numOps + 1; return result; } } |
Output
Elapsed count f( 8): 7: 2.333 [ 0.000 : NaN] Elapsed count f( 16): 15: 2.143 [ 0.000 : NaN] Elapsed count f( 32): 31: 2.067 [ 0.000 : NaN] Elapsed count f( 64): 63: 2.032 [ 0.000 : NaN] Elapsed count f( 128): 127: 2.016 [ 0.000 : NaN] Elapsed count f( 256): 255: 2.008 [ 0.000 : NaN] Elapsed count f( 512): 511: 2.004 [ 0.000 : NaN] Elapsed count f( 1,024): 1,023: 2.002 [ 0.000 : NaN] Elapsed count f( 2,048): 2,047: 2.001 [ 0.000 : NaN] Elapsed count f( 4,096): 4,095: 2.000 [ 0.000 : NaN] Elapsed count f( 8,192): 8,191: 2.000 [ 0.000 : NaN]
This is linear: ~ N
| Recursive Fibonacci (Terrible Version) [17/19] |
01 |
public static long f (long N) { if (N <= 1) { return N; } else { long result = f(N-1) + f(N-2); numOps = numOps + 1; return result; } } |
Output
Elapsed count f( 8): 33: 8.250 [ 0.000 : NaN] Elapsed count f( 16): 1,596: 48.364 [ 0.000 : NaN] Elapsed count f( 32): 3,524,577: 2208.382 [ 0.011 : Infinity] Elapsed count f( 64) aborted execution after a thousand hours or so Elapsed count f( 128) aborted execution after a thousand hours or so Elapsed count f( 256) aborted execution after a thousand hours or so Elapsed count f( 512) aborted execution after a thousand hours or so Elapsed count f( 1,024) aborted execution after a thousand hours or so Elapsed count f( 2,048) aborted execution after a thousand hours or so Elapsed count f( 4,096) aborted execution after a thousand hours or so Elapsed count f( 8,192) aborted execution after a thousand hours or so
This is exponential: approximately 2^N
More accurately:
(1.6)^N, where 1.6 = (1+sqrt(5))/2
| String Concatenation (Recursive) [18/19] |
01 |
public static String f (long N) { if (N == 0) { return ""; } else { String result = "*" + f(N - 1); numOps = numOps + result.length(); return result; } } |
Output
Elapsed count f( 8): 36: 3.600 [ 0.000 : NaN] Elapsed count f( 16): 136: 3.778 [ 0.000 : NaN] Elapsed count f( 32): 528: 3.882 [ 0.000 : NaN] Elapsed count f( 64): 2,080: 3.939 [ 0.001 : Infinity] Elapsed count f( 128): 8,256: 3.969 [ 0.000 : 0.000] Elapsed count f( 256): 32,896: 3.984 [ 0.000 : NaN] Elapsed count f( 512): 131,328: 3.992 [ 0.000 : NaN] Elapsed count f( 1,024): 524,800: 3.996 [ 0.001 : Infinity] Elapsed count f( 2,048): 2,098,176: 3.998 [ 0.003 : 3.000] Elapsed count f( 4,096): 8,390,656: 3.999 [ 0.012 : 4.000]
Exception in thread "main" java.lang.StackOverflowError at java.base/java.lang.StringBuilder.<init>(StringBuilder.java:124) at algs14.XCountingRecursion.f(XCountingRecursion.java:18)
| String Concatenation (Loop) [19/19] |
01 |
public static String f (long N) { String result = ""; while (N != 0) { N = N - 1; result = "*" + result; numOps = numOps + result.length(); } return result; } |
Output
Elapsed count f( 8): 36: 3.600 [ 0.000 : NaN] Elapsed count f( 16): 136: 3.778 [ 0.000 : NaN] Elapsed count f( 32): 528: 3.882 [ 0.000 : NaN] Elapsed count f( 64): 2,080: 3.939 [ 0.000 : NaN] Elapsed count f( 128): 8,256: 3.969 [ 0.000 : NaN] Elapsed count f( 256): 32,896: 3.984 [ 0.000 : NaN] Elapsed count f( 512): 131,328: 3.992 [ 0.000 : NaN] Elapsed count f( 1,024): 524,800: 3.996 [ 0.001 : Infinity] Elapsed count f( 2,048): 2,098,176: 3.998 [ 0.003 : 3.000] Elapsed count f( 4,096): 8,390,656: 3.999 [ 0.010 : 3.333] Elapsed count f( 8,192): 33,558,528: 4.000 [ 0.041 : 4.100] Elapsed count f( 16,384): 134,225,920: 4.000 [ 0.077 : 1.878] Elapsed count f( 32,768): 536,887,296: 4.000 [ 0.181 : 2.351] Elapsed count f( 65,536): 2,147,516,416: 4.000 [ 0.517 : 2.856] Elapsed count f( 131,072): 8,590,000,128: 4.000 [ 0.847 : 1.638] Elapsed count f( 262,144): 34,359,869,440: 4.000 [ 3.567 : 4.211] Elapsed count f( 524,288): 137,439,215,616: 4.000 [ 13.881 : 3.892] Elapsed count f( 1,048,576): 549,756,338,176: 4.000 [ 62.358 : 4.492]
This is quadratic: approximately N^2
Revised: 2008/03/17 13:01